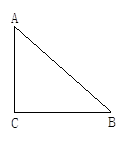一服装厂里有大量形状为等腰直角三角形的边角布料,如图所示,现找出其中一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形, 做成形状不同的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切, 请设计出所有可能符合题意的方案示意图,并直接写出扇形的半径.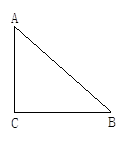
相关试题
时，求代数式
的值。（本题6分）探索与思考：
观察下列等式：
……………………（1）想一想：等式左边各项幂的底数与右边幂的底数有什么关系？
（2）试一试：13 + 23 + 3 3 + 43 + … + 10 3= ____________．
（3）猜一猜：可得出什么规律（可用带字母的等式表示，也可用文字表述）：
，试求
的值。
,
,
,
,
,
。
粤公网安备 44130202000953号