如图,点M是反比例函数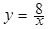 在第一象限内图象上的点,
在第一象限内图象上的点,
作MB⊥x轴于点B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=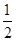 A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=
A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=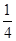 A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=
A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=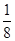 A3M, △A3C3B的面积记为S3;依次类推…;则S1+S2+S3= .
A3M, △A3C3B的面积记为S3;依次类推…;则S1+S2+S3= .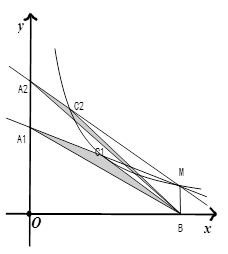
相关知识点
推荐套卷
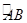 上两点,且∠MEB= ∠NFB= 60°,则EM+FN= .
上两点,且∠MEB= ∠NFB= 60°,则EM+FN= .


 粤公网安备 44130202000953号
粤公网安备 44130202000953号