如图，已知圆O的直径AB=4，定直线L到圆心的距离为4，且直线L⊥直线AB。点P是圆O上异于A、B的任意一点，直线PA、PB分别交L与M、N点。试建立适当的直角坐标系，解决下列问题：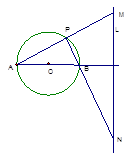
（1）若∠PAB=30°，求以MN为直径的圆方程；
（2）当点P变化时，求证：以MN为直径的圆必过圆O内的一定点。
相关试题
时，求
的值；
在
上的值域.
如图，矩形
的长
，宽
，
，
两点分别在
，
轴的正半轴上移动，
，
两点在第一象限.求
的最大值.
.
的最大值及单调增区间；
，
.
，求证：
；
的值.
的终边经过点
，且
，求
，
的值．推荐套卷
如图，已知圆O的直径AB=4，定直线L到圆心的距离为4，且直线L⊥直线AB。点P是圆O上异于A、B的任意一点，直线PA、PB分别交L与M、N点。试建立适当的直角坐标系，解决下列问题：
（1）若∠PAB=30°，求以MN为直径的圆方程；
（2）当点P变化时，求证：以MN为直径的圆必过圆O内的一定点。
粤公网安备 44130202000953号