有甲,乙两个盒子,甲盒中装有2个小球,乙盒中装有3个小球,每次随机选取一个盒子并从中取出一个小球
(1)当甲盒中的球被取完时,求乙盒中恰剩下1个球的概率;
(2)当第一次取完一个盒子中的球时,另一个盒子恰剩下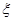 个球,求
个球,求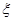 的分布列及期望
的分布列及期望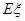 。
。
相关知识点
推荐套卷
有甲,乙两个盒子,甲盒中装有2个小球,乙盒中装有3个小球,每次随机选取一个盒子并从中取出一个小球
(1)当甲盒中的球被取完时,求乙盒中恰剩下1个球的概率;
(2)当第一次取完一个盒子中的球时,另一个盒子恰剩下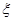 个球,求
个球,求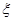 的分布列及期望
的分布列及期望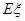 。
。