(本题满分14分,第1小题6分,第2小题8分)
已知函数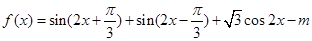 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
推荐套卷
(本题满分14分,第1小题6分,第2小题8分)
已知函数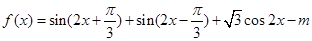 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.