如图,已知抛物线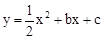 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(1)b=,点B的横坐标为(上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线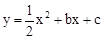 交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
交于点E.点D是x轴上一点,其坐标为(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有个.