如图，在矩形ABCD中，AC与BD相交于O，∠COD=60°，点E是BC边上的动点，连结DE，OE．
（1）求证：△COD是等边三角形；
（2）如图1，当DE平分∠ADC时，试证明OC=EC，并求出∠DOE的度数；
（3）如图2，当DE平分∠BDC时，试证明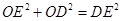
．
相关知识点
推荐套卷
如图，在矩形ABCD中，AC与BD相交于O，∠COD=60°，点E是BC边上的动点，连结DE，OE．
（1）求证：△COD是等边三角形；
（2）如图1，当DE平分∠ADC时，试证明OC=EC，并求出∠DOE的度数；
（3）如图2，当DE平分∠BDC时，试证明．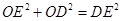
粤公网安备 44130202000953号