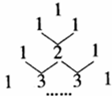
右图是我国古代数学家杨辉最早发现的,称为“杨辉三角形”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角形”中有许多规律,如它的每一行的数字正好对应了 (
(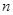 为非负整数)的展开式中
为非负整数)的展开式中 按次数从大到小排列的项的系数.例如
按次数从大到小排列的项的系数.例如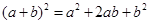 展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
展开式中的系数1、2、1恰好对应图中第三行的数字;再如, 展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出
展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出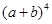 的展开式.
的展开式.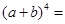 .
.
右图是我国古代数学家杨辉最早发现的,称为“杨辉三角形”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角形”中有许多规律,如它的每一行的数字正好对应了 (
(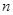 为非负整数)的展开式中
为非负整数)的展开式中 按次数从大到小排列的项的系数.例如
按次数从大到小排列的项的系数.例如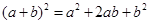 展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
展开式中的系数1、2、1恰好对应图中第三行的数字;再如, 展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出
展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出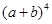 的展开式.
的展开式.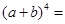 .
.