(1)正三角形,(2)正四边形,(3)正五边形,(4)正六边形,(5)正八边形,(6)正九边形都是轴对称图形,数一数它们的对称轴的条数.观察后分析:正多边形对称轴的条数与边数n有什么关系?根据你的分析结果回答,正十边形,正十六边形,正二十九边形分别有几条对称轴?正五十边形呢?正一百边形呢?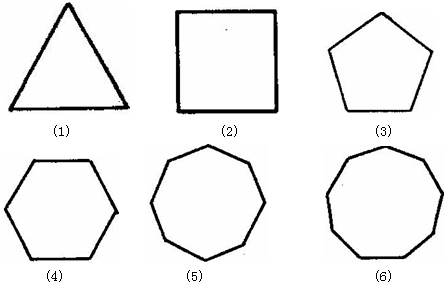
(1)正三角形,(2)正四边形,(3)正五边形,(4)正六边形,(5)正八边形,(6)正九边形都是轴对称图形,数一数它们的对称轴的条数.观察后分析:正多边形对称轴的条数与边数n有什么关系?根据你的分析结果回答,正十边形,正十六边形,正二十九边形分别有几条对称轴?正五十边形呢?正一百边形呢?