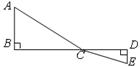
如图,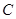 为线段
为线段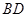 上一动点,分别过点
上一动点,分别过点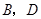 作
作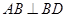 ,
,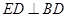 ,连接
,连接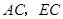 .已知
.已知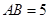 ,
,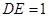 ,
,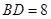 ,设
,设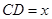 .
.
(1)用含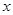 的代数式表示
的代数式表示 的长;
的长;
(2)请问点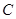 满足什么条件时,
满足什么条件时, 的值最小?
的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式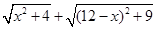 的最小值.
的最小值.
相关知识点
推荐套卷
如图,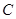 为线段
为线段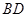 上一动点,分别过点
上一动点,分别过点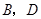 作
作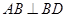 ,
,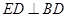 ,连接
,连接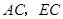 .已知
.已知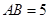 ,
,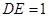 ,
,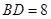 ,设
,设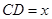 .
.
(1)用含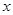 的代数式表示
的代数式表示 的长;
的长;
(2)请问点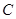 满足什么条件时,
满足什么条件时, 的值最小?
的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式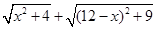 的最小值.
的最小值.