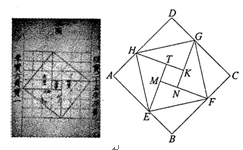
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到,它是用八个全等的直角三角形拼接而成，记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3＝10,则S2的值是( )
| A．5 | B． |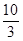
C．3 | D．4 |
相关试题
1
的结果是（）
相关知识点
推荐套卷
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到,它是用八个全等的直角三角形拼接而成，记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3＝10,则S2的值是( )
| A．5 | B． |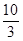
C．3 | D．4 |
粤公网安备 44130202000953号