如图,是小王骑自行车离家的距离S(千米)与时间t (小时)之间的变化关系.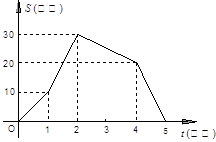
(1)根据图形填表:
| 时间t(小时) |
0 |
1 |
2 |
3 |
4 |
5 |
| 距离S(千米) |
|
|
|
|
|
|
(2)小王离家最远时是什么的时刻?这时离家有多远?
(3)他骑自行车最快的速度是多少?最慢的速度是多少?
(4)小王在哪一时刻与家相距20千米?
如图,是小王骑自行车离家的距离S(千米)与时间t (小时)之间的变化关系.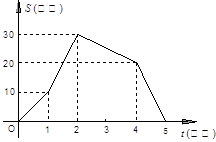
(1)根据图形填表:
| 时间t(小时) |
0 |
1 |
2 |
3 |
4 |
5 |
| 距离S(千米) |
|
|
|
|
|
|
(2)小王离家最远时是什么的时刻?这时离家有多远?
(3)他骑自行车最快的速度是多少?最慢的速度是多少?
(4)小王在哪一时刻与家相距20千米?