（本小题共12分）已知f(x)=m(x-2m)（x+m+3）,g(x)=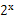
-2，若同时满足条件：
①
x∈R，f(x) ＜0或g(x) ＜0；②
x∈(﹣∝, ﹣4),f(x)g(x) ＜0。求m的取值范围。
相关试题
，且
，
（1）判断函数
的奇偶性；（2）判断
上的单调性并加以证明．
的顶点在原点，始边与x轴正半轴重合，终边为射线4x＋3y＝0（x≥0），求5sin
．其中
．
＝
的定义域为
，集合
＝
，
，求
的取值范围．
;⑵
．
（
，
），
．
时，对于任意不相等的两个正实数
、
，均有
成立；
，若
在
上单调递增，求实数
的取值范围；相关知识点
推荐套卷
（本小题共12分）已知f(x)=m(x-2m)（x+m+3）,g(x)=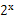-2，若同时满足条件：
①x∈R，f(x) ＜0或g(x) ＜0；②x∈(﹣∝, ﹣4),f(x)g(x) ＜0。求m的取值范围。
粤公网安备 44130202000953号