如图, 信封中装有两张卡片,卡片上分别写着7cm、3cm;
信封中装有两张卡片,卡片上分别写着7cm、3cm; 信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.用画树状图法,求这三条线段能组成三角形的概率.
信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.用画树状图法,求这三条线段能组成三角形的概率.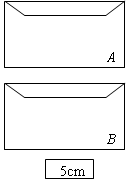
相关知识点
推荐套卷
如图, 信封中装有两张卡片,卡片上分别写着7cm、3cm;
信封中装有两张卡片,卡片上分别写着7cm、3cm; 信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.用画树状图法,求这三条线段能组成三角形的概率.
信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.用画树状图法,求这三条线段能组成三角形的概率.