(本小题14分) 如图，在平面直角坐标系xoy中，设点F(0, p)(p>0), 直线l : y= －p, 点P在直线l上移动，R是线段PF与x轴的交点, 过R、P分别作直线
、
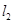，使
，
.
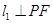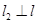
(1)求动点Q的轨迹C的方程；
(2)在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
(3)对(2)求证：当直线MA, MF, MB的斜率存在时，直线MA, MF, MB的斜率的倒数成等差数列.
关于直线
对称的直线方程．
表示的平面区域，并求其面积．
过两点
和
，求
，
，
，如图所示，若直线
过
点且与线段
公共点，试求直线
的取值范围．
且和直线
垂直的直线的方程．推荐套卷
(本小题14分) 如图，在平面直角坐标系xoy中，设点F(0, p)(p>0), 直线l : y= －p, 点P在直线l上移动，R是线段PF与x轴的交点, 过R、P分别作直线、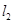，使， .
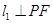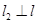
(1)求动点Q的轨迹C的方程；
(2)在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
(3)对(2)求证：当直线MA, MF, MB的斜率存在时，直线MA, MF, MB的斜率的倒数成等差数列.
粤公网安备 44130202000953号