如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.

(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
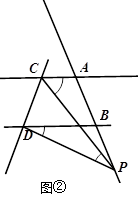
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)