已知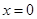
是函数
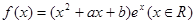的一个极值点，且函数
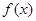的图象在
处的切线的斜率为2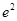
.
（Ⅰ）求函数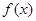的解析式并求单调区间.
（Ⅱ）设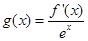
，其中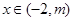
，问：对于任意的
,方程
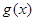
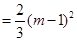在区间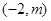
上是否存在实数根？若存在，请确定实数根的个数.若不存在，请说明理由.
≥
(a＋b)．
；
, 若p是q的充分非必要条件，求实数
的取值范围。
满足
为实数（
为虚数单位），且
，求
，集合
=
， 
求：
推荐套卷
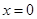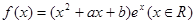已知是函数的一个极值点，且函数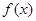的图象在处的切线的斜率为2.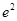
（Ⅰ）求函数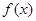的解析式并求单调区间.
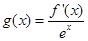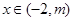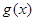
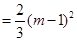（Ⅱ）设，其中，问：对于任意的,方程在区间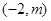上是否存在实数根？若存在，请确定实数根的个数.若不存在，请说明理由.
粤公网安备 44130202000953号