有一塔形几何体由若干个正方体构成, 构成方式如图所示: 上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点. 已知最上层正方体的棱长为2, 且该塔形几何体的表面积(不含重叠部分，含最底层正方体的底面面积)超过39, 则该塔形中正方体的个数至少是______个.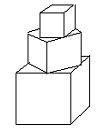
中，x的取值范围是________．
．
，则(－xy)2＝________．
．
．相关知识点
推荐套卷
有一塔形几何体由若干个正方体构成, 构成方式如图所示: 上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点. 已知最上层正方体的棱长为2, 且该塔形几何体的表面积(不含重叠部分，含最底层正方体的底面面积)超过39, 则该塔形中正方体的个数至少是______个.
粤公网安备 44130202000953号