在直角坐标系中,A(-3,4),B(-1,-2),O为原点.
(1)求△AOB的面积;
(2)将这个三角形向上平移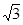 个单位长度,得△A/O/B/ ,再作△A/O/B/ 关于
个单位长度,得△A/O/B/ ,再作△A/O/B/ 关于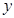 轴的对称图形△A//O//B//,试写出△A/O/B/ 和△A//O//B//各顶点的坐标.
轴的对称图形△A//O//B//,试写出△A/O/B/ 和△A//O//B//各顶点的坐标.
相关知识点
推荐套卷
在直角坐标系中,A(-3,4),B(-1,-2),O为原点.
(1)求△AOB的面积;
(2)将这个三角形向上平移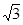 个单位长度,得△A/O/B/ ,再作△A/O/B/ 关于
个单位长度,得△A/O/B/ ,再作△A/O/B/ 关于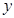 轴的对称图形△A//O//B//,试写出△A/O/B/ 和△A//O//B//各顶点的坐标.
轴的对称图形△A//O//B//,试写出△A/O/B/ 和△A//O//B//各顶点的坐标.