给出以下四个命题：
①“若x＋y=0，则x，y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
③“若
，则
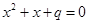有实根”的逆否命题；
④“不等边三角形的三内角相等”的逆否命题．
其中真命题是 ( )
| A．①② | B．②③ |
| C．①③ | D．③④ |
相关试题
是定义在
上偶函数，则
在区间［0,2］上是（ ）
，若
，则
的值是（）
，
；
，
；
，
；
，
；
，
。
，则集合
的真子集共有（）
个
个
个
个推荐套卷
给出以下四个命题：
①“若x＋y=0，则x，y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
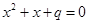③“若，则有实根”的逆否命题；
④“不等边三角形的三内角相等”的逆否命题．
其中真命题是 ( )
| A．①② | B．②③ |
| C．①③ | D．③④ |
粤公网安备 44130202000953号