如图,抛物线y=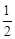 x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).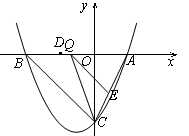
(1)求抛物线的解析式;
(2)点Q是线段OB上的动点,过点Q作QE//BC,交AC于点E,连接CQ,设OQ=m,当△CQE的面积最大时,求m的值,并写出点Q的坐标.
(3)若平行于x轴的动直线,与该抛物线交于点P,与直线BC交于点F,D的坐标为(-2,0),则是否存在这样的直线l,使OD=DF?若存在,求出点P的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
 .
.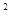 —6x+9=(5—2x)
—6x+9=(5—2x) =4y+2
=4y+2 +2
+2 x+1=0
x+1=0
 粤公网安备 44130202000953号
粤公网安备 44130202000953号