（本小题满分13分）设椭圆
的左、右焦点分别为F1、F2，上顶点为A，在x轴上有一点B，满足
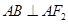且F1为BF2的中点.
（Ⅰ）求椭圆 C的离心率；
（Ⅱ）若过A、B、F2三点的圆恰好与直线
相切，判断椭圆C和直线
的位置关系.
相关试题
．
的展开式的二项式系数和为128．
的值; 
在
时有极值0。
的范围。
中，已知
，且
。
；
．推荐套卷
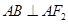（本小题满分13分）设椭圆的左、右焦点分别为F1、F2，上顶点为A，在x轴上有一点B，满足且F1为BF2的中点.
（Ⅰ）求椭圆 C的离心率；
（Ⅱ）若过A、B、F2三点的圆恰好与直线相切，判断椭圆C和直线的位置关系.
粤公网安备 44130202000953号