(本小题满分12分)已知函数y=|cosx+sinx|.
(1)画出函数在x∈[-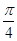 ,
,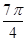 ]上的简图;
]上的简图;
(2)写出函数的最小正周期和在[-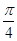 ,
, ]上的单调递增区间;试问:当x在R上取何值
]上的单调递增区间;试问:当x在R上取何值
时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
推荐套卷
(本小题满分12分)已知函数y=|cosx+sinx|.
(1)画出函数在x∈[-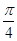 ,
,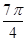 ]上的简图;
]上的简图;
(2)写出函数的最小正周期和在[-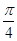 ,
, ]上的单调递增区间;试问:当x在R上取何值
]上的单调递增区间;试问:当x在R上取何值
时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.