(本小题满分12分)
设A1、A2是双曲线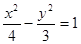 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于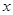 轴的弦,
轴的弦,
(Ⅰ)直线A1P1与A2P2交点P的轨迹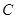 的方程;
的方程;
(Ⅱ)过 与
与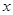 轴的交点Q作直线与(1)中轨迹
轴的交点Q作直线与(1)中轨迹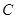 交于M、N两点,连接FN、FM,其中F
交于M、N两点,连接FN、FM,其中F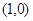 ,求证:
,求证: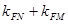 为定值;
为定值;
相关知识点
推荐套卷
(本小题满分12分)
设A1、A2是双曲线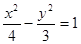 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于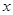 轴的弦,
轴的弦,
(Ⅰ)直线A1P1与A2P2交点P的轨迹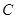 的方程;
的方程;
(Ⅱ)过 与
与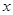 轴的交点Q作直线与(1)中轨迹
轴的交点Q作直线与(1)中轨迹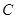 交于M、N两点,连接FN、FM,其中F
交于M、N两点,连接FN、FM,其中F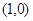 ,求证:
,求证: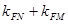 为定值;
为定值;