已知关于x的二次函数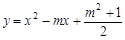
与
，这两个二次函数的图象中的一条与x轴交于A，B两个不同的点.
（1）试判断哪个二次函数的图象可能经过A，B两点；
（2）若A点坐标为（－1，0），试求出B点坐标；
（3）在（2）的条件下，对于经过A，B两点的二次函数，当x取何值时， y的值随x值的增大而减小．
，求
的值
比－
的值大1？
、
轴上找一点C，是C点到A、B的距离之和最短，求C点坐标；
、
，当四边形ABNM的周长最短是，求
的值。
为
与直线
相交于A点，直线
轴于B点，直线
交
轴于C点，求① A点的坐标；② △ABC的面积。
相关知识点
推荐套卷
已知关于x的二次函数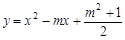与，这两个二次函数的图象中的一条与x轴交于A，B两个不同的点.
（1）试判断哪个二次函数的图象可能经过A，B两点；
（2）若A点坐标为（－1，0），试求出B点坐标；
（3）在（2）的条件下，对于经过A，B两点的二次函数，当x取何值时， y的值随x值的增大而减小．
粤公网安备 44130202000953号