作图题如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC
(顶点是网格线的交点)和点A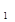 。
。
(1)画出一个格点△A 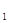 B
B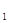 C
C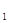 ,使它与△ABC全等,且A与 A
,使它与△ABC全等,且A与 A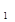 是对应点。
是对应点。
(2)画出点B关于直线AC的对称点D,并指出AD 可以看作由AB绕A点经过怎样的旋转而得到的。
相关知识点
推荐套卷
作图题如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC
(顶点是网格线的交点)和点A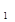 。
。
(1)画出一个格点△A 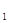 B
B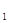 C
C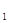 ,使它与△ABC全等,且A与 A
,使它与△ABC全等,且A与 A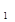 是对应点。
是对应点。
(2)画出点B关于直线AC的对称点D,并指出AD 可以看作由AB绕A点经过怎样的旋转而得到的。