某公司向银行贷款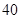 万元,用来生产某种产品,已知该贷款的利率为
万元,用来生产某种产品,已知该贷款的利率为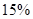 (不计复利,即还贷款前两年利息不计算),每个新产品的成本是
(不计复利,即还贷款前两年利息不计算),每个新产品的成本是 元,售价是
元,售价是 元,应纳税款是销售额的
元,应纳税款是销售额的 ,如果每年生产该种产品
,如果每年生产该种产品 万个,并把所得利润(利润=销售额-成本-应纳税款)用来归还贷款,问需要几年后才能一次性还清?
万个,并把所得利润(利润=销售额-成本-应纳税款)用来归还贷款,问需要几年后才能一次性还清?
某公司向银行贷款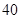 万元,用来生产某种产品,已知该贷款的利率为
万元,用来生产某种产品,已知该贷款的利率为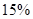 (不计复利,即还贷款前两年利息不计算),每个新产品的成本是
(不计复利,即还贷款前两年利息不计算),每个新产品的成本是 元,售价是
元,售价是 元,应纳税款是销售额的
元,应纳税款是销售额的 ,如果每年生产该种产品
,如果每年生产该种产品 万个,并把所得利润(利润=销售额-成本-应纳税款)用来归还贷款,问需要几年后才能一次性还清?
万个,并把所得利润(利润=销售额-成本-应纳税款)用来归还贷款,问需要几年后才能一次性还清?