(本小题满分14分)
已知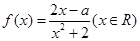
(1)当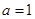 时,求曲线
时,求曲线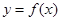 在点
在点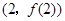 处的切线方程;
处的切线方程;
(2)若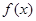 在区间
在区间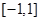 上是增函数,求实数
上是增函数,求实数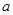 的取值范围
的取值范围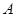 ;
;
(3)在(2)的条件下,设关于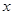 的方程
的方程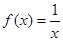 的两个根为
的两个根为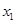 、
、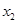 ,若对任意
,若对任意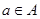 ,
,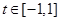 ,不等式
,不等式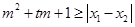 恒成立,求
恒成立,求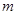 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分14分)
已知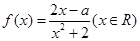
(1)当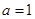 时,求曲线
时,求曲线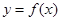 在点
在点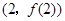 处的切线方程;
处的切线方程;
(2)若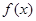 在区间
在区间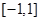 上是增函数,求实数
上是增函数,求实数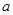 的取值范围
的取值范围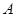 ;
;
(3)在(2)的条件下,设关于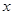 的方程
的方程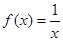 的两个根为
的两个根为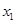 、
、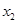 ,若对任意
,若对任意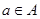 ,
,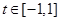 ,不等式
,不等式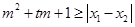 恒成立,求
恒成立,求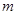 的取值范围.
的取值范围.