为了解某校“振兴阅读工程”的开展情况,教育部门对该校初中生的
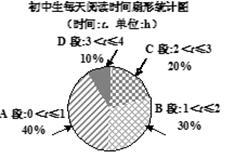

阅读情况进行了随机问卷调查,绘制了如下图表:
初中生喜爱的文学作品种类调查统计表
种类
|
小说
|
散文
|
传记
|
科普
|
军事
|
诗歌
|
其他
|
人数
|
72
|
8
|
21
|
19
|
15
|
2
|
13
|
根据上述图表提供的信息,解答下列问题:
(1)喜爱小说的人数占被调查人数的百分比是多少?初中生每天阅读时间的中位数在哪
个时间段内?
(2)将写读后感、笔记积累、画圈点读等三种方式称为有记忆阅读.请估计该校现有的
2000名初中生中,能进行有记忆阅读的人数约是多少?