如图所示的地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出一种用多边形 (不一定是正多边形)的材料铺地面的方案?把你想到的方案画成草图.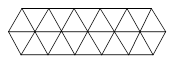
如图所示的地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出一种用多边形 (不一定是正多边形)的材料铺地面的方案?把你想到的方案画成草图.