如图,已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC="90°" , ②OC=OE， ③tan∠OCD =
，④
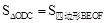中，正确的有【 】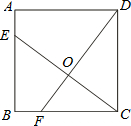
A.1个 B.2个 C.3个 D.4个
相关试题
的计算结果为( )
，N=
，则M，N的大小关系是（）
+
＝0中，y为负数，则m的取值范围是（）
中的
和
都扩大3倍，那么分式的值（）相关知识点
推荐套卷
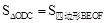如图,已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC="90°" , ②OC=OE， ③tan∠OCD = ，④ 中，正确的有【 】
A.1个 B.2个 C.3个 D.4个
粤公网安备 44130202000953号