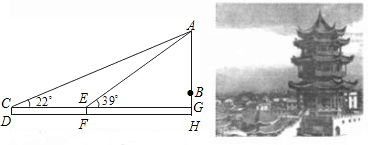
极具特色的“八卦楼”(又称“威镇阁”)是漳州的标志性建筑,它建立在一座平台上.为了测量“八卦楼”的高度AB,小华在D处用高1.1米的测角仪CD,测得楼的顶端A的仰角为22o;再向前走63米到达F处,又测得楼的顶端A的仰角为39o(如图是他设计的平面示意图).已知平台的高度BH约为13米,请你求出“八卦楼”的高度约多少米?
(参考数据:sin22o≈ ,tan220≈
,tan220≈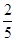 ,sin39o≈
,sin39o≈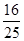 ,tan39o≈
,tan39o≈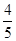 )
) 
相关知识点
推荐套卷
极具特色的“八卦楼”(又称“威镇阁”)是漳州的标志性建筑,它建立在一座平台上.为了测量“八卦楼”的高度AB,小华在D处用高1.1米的测角仪CD,测得楼的顶端A的仰角为22o;再向前走63米到达F处,又测得楼的顶端A的仰角为39o(如图是他设计的平面示意图).已知平台的高度BH约为13米,请你求出“八卦楼”的高度约多少米?
(参考数据:sin22o≈ ,tan220≈
,tan220≈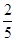 ,sin39o≈
,sin39o≈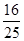 ,tan39o≈
,tan39o≈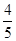 )
) 