已知抛物线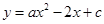 与它的对称轴相交于点
与它的对称轴相交于点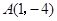 ,与
,与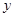 轴交于
轴交于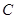 ,与
,与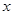 轴正半轴交于
轴正半轴交于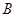 .
.
(1)求这条抛物线的函数关系式;
(2)设直线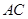 交
交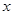 轴于
轴于 是线段
是线段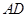 上一动点(
上一动点(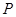 点异于
点异于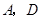 ),过
),过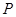 作
作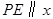 轴交直线
轴交直线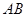 于
于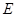 ,过
,过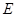 作
作 轴于
轴于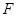 ,求当四边形
,求当四边形 的面积等于
的面积等于 时点
时点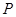 的坐标.
的坐标.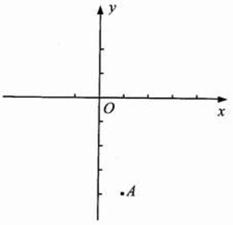
相关知识点
推荐套卷
已知抛物线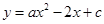 与它的对称轴相交于点
与它的对称轴相交于点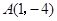 ,与
,与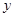 轴交于
轴交于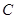 ,与
,与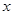 轴正半轴交于
轴正半轴交于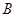 .
.
(1)求这条抛物线的函数关系式;
(2)设直线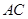 交
交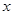 轴于
轴于 是线段
是线段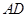 上一动点(
上一动点(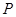 点异于
点异于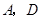 ),过
),过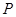 作
作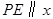 轴交直线
轴交直线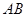 于
于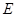 ,过
,过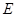 作
作 轴于
轴于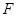 ,求当四边形
,求当四边形 的面积等于
的面积等于 时点
时点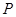 的坐标.
的坐标.