某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.下图是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:(1)该校对多少名学生进行了抽样调查?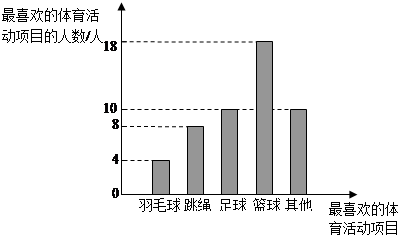
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少 ?
相关知识点
推荐套卷
某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.下图是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少 ?