如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.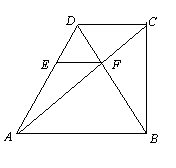
⑴求证：四边形ABFE是等腰梯形;
⑵求AE的长.
中，
是高，
，
分别是
和
的平分线，它们相交于点
，
，
。求
，
。
∥
，
。
。
，并将它的解集在数轴上表示出来。
，并写出它的非正整数解。
相关知识点
推荐套卷
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.
⑴求证：四边形ABFE是等腰梯形;
⑵求AE的长.
粤公网安备 44130202000953号