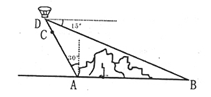
如图,在小山的西侧A处有一热气球,以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空,40分钟后到达C处,这时热气球上的人发现,在A处的正东方向有一处着火点B,十分钟后,在D处测得着火点B的俯角为15°,求热气球升空点A与着火点B的距离。(结果保留根号,参考数据:
(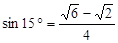 ,
,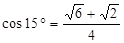 ,
,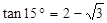 ,
, )。
)。
相关知识点
推荐套卷
如图,在小山的西侧A处有一热气球,以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空,40分钟后到达C处,这时热气球上的人发现,在A处的正东方向有一处着火点B,十分钟后,在D处测得着火点B的俯角为15°,求热气球升空点A与着火点B的距离。(结果保留根号,参考数据:
(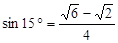 ,
,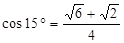 ,
,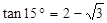 ,
, )。
)。