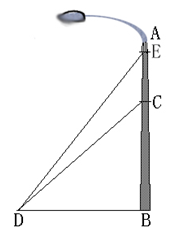
如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,则 BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
【参考数据: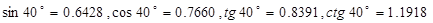 】
】
相关知识点
推荐套卷
如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,则 BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
【参考数据: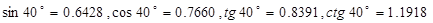 】
】