如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的是 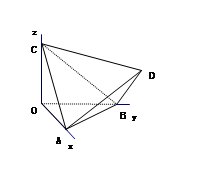
A.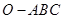 是正三棱锥 是正三棱锥 |
B.直线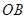 ∥平面ACD ∥平面ACD |
C.直线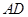 与 与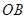 所成的角是 所成的角是 |
D.二面角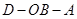 为 为 . . |
相关知识点
推荐套卷
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的是 
A.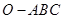 是正三棱锥 是正三棱锥 |
B.直线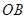 ∥平面ACD ∥平面ACD |
C.直线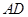 与 与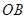 所成的角是 所成的角是 |
D.二面角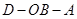 为 为 . . |