《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一。书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的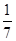
是较小的两份之和，问最小1份为（ ）
A． |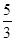
B． |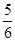
C． |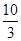
D． |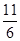
相关试题
与
的交点的横坐标是
，则
）
与
与
与
与
，其中法则
．若
，则集合
可以为（）
相关知识点
推荐套卷
《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一。书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的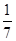是较小的两份之和，问最小1份为（ ）
| A． |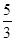
B． |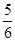
C． |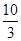
D． |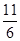
粤公网安备 44130202000953号