如图，在梯形ABCD中，AB∥CD，∠BAD=90°，以AD为直径的半圆D与BC相切。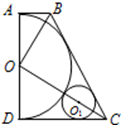
（1）求证：OB⊥OC；
（2）若AD=12，∠BCD=60°，⊙O1与半⊙O外切，并与BC、CD相切，求⊙O1的面积。
，然后取你喜欢的一组
的值代入求值（提示：所取的值必须使代数式有意义）
，求
的值？
相关知识点
推荐套卷
如图，在梯形ABCD中，AB∥CD，∠BAD=90°，以AD为直径的半圆D与BC相切。
（1）求证：OB⊥OC；
（2）若AD=12，∠BCD=60°，⊙O1与半⊙O外切，并与BC、CD相切，求⊙O1的面积。
粤公网安备 44130202000953号