如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为ts(0<t<6),试尝试探究下列问题:
(1)当t为何值时,△PBQ的面积等于8cm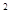 ?
?
(2)求证:四边形PBQD面积为定值.
(3)当t为何值时,△PDQ是等腰三角形?写出探索过程.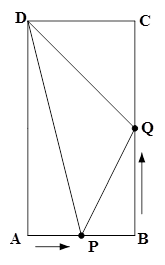
相关知识点
推荐套卷
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为ts(0<t<6),试尝试探究下列问题:
(1)当t为何值时,△PBQ的面积等于8cm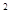 ?
?
(2)求证:四边形PBQD面积为定值.
(3)当t为何值时,△PDQ是等腰三角形?写出探索过程.