已知函数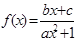 (
( )是奇函数,
)是奇函数, 有最大值
有最大值
且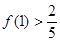 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在直线 与
与 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得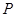 、
、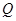 两点关于点
两点关于点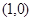 对称,若存在,求出直线
对称,若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
相关知识点
推荐套卷
已知函数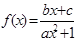 (
( )是奇函数,
)是奇函数, 有最大值
有最大值
且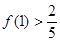 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在直线 与
与 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得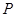 、
、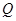 两点关于点
两点关于点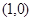 对称,若存在,求出直线
对称,若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.