如图所示,在Rt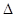 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt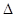 ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt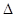 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt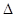 ADE,求出Rt
ADE,求出Rt ADE 的直角边DE被⊙M截得的弦PQ的长度;
ADE 的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)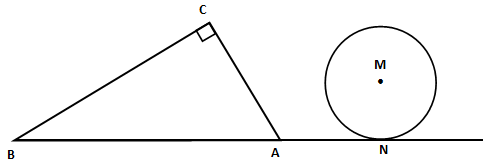
相关知识点
推荐套卷
如图所示,在Rt ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt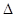 ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt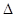 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt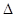 ADE,求出Rt
ADE,求出Rt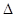 ADE 的直角边DE被⊙M截得的弦PQ的长度;
ADE 的直角边DE被⊙M截得的弦PQ的长度;
(2)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)