如图,AD是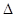 ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
(1)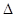 ASR与
ASR与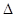 ABC相似吗?为什么?
ABC相似吗?为什么?
(2)求正方形PQRS的边长。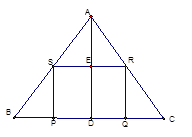
相关知识点
推荐套卷
如图,AD是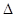 ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
(1)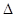 ASR与
ASR与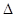 ABC相似吗?为什么?
ABC相似吗?为什么?
(2)求正方形PQRS的边长。