已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F ,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
⑴ 求证:△BCE≌△DCF;
⑵ OG与BF有什么数量关系?证明你的结论;
⑶ 若GE·GB=4-2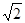 ,求 正方形ABCD的面积.
,求 正方形ABCD的面积.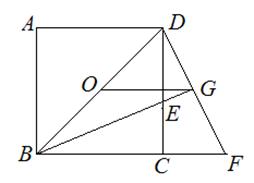
相关知识点
推荐套卷
已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F ,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
⑴ 求证:△BCE≌△DCF;
⑵ OG与BF有什么数量关系?证明你的结论;
⑶ 若GE·GB=4-2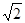 ,求 正方形ABCD的面积.
,求 正方形ABCD的面积.