正方形 的边长为4,
的边长为4,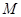 、
、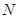 分别是
分别是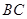 、
、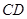 上的两个动点,当
上的两个动点,当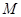 点在
点在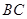 上运动时,始终保持
上运动时,始终保持 和
和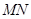 垂直,
垂直,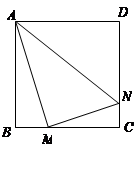
(1)证明: ;
;
(2)设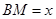 ,梯形
,梯形 的面积为
的面积为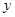 ,求
,求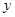 与
与 之间的函数关系式;当
之间的函数关系式;当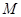 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当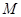 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.
相关知识点
推荐套卷
正方形 的边长为4,
的边长为4,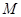 、
、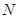 分别是
分别是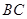 、
、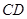 上的两个动点,当
上的两个动点,当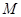 点在
点在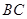 上运动时,始终保持
上运动时,始终保持 和
和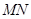 垂直,
垂直,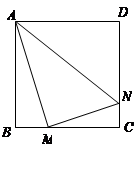
(1)证明: ;
;
(2)设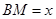 ,梯形
,梯形 的面积为
的面积为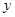 ,求
,求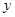 与
与 之间的函数关系式;当
之间的函数关系式;当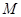 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当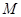 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.