请尝试解决以下问题:
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,
由旋转可得:AB="AD,BG=DE," ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.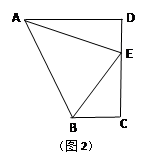
(3)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD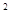 +CE
+CE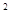 =DE
=DE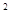 始终成立,请说明理由.
始终成立,请说明理由.
相关知识点
推荐套卷
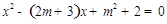 .
.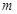 的取值范围;
的取值范围;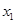 ,
,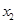 ,且满足
,且满足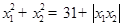 ,求实数
,求实数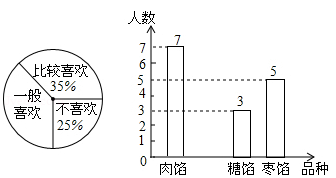

 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号