(本小题满分16分)
如图，椭圆
(a>b>0)的上、下两个顶点为A、B，直线l：
，点P是椭圆上异于点A、B的任意一点，连接AP并延长交直线l于点N，连接PB并延长交直线l于点M，设AP所在的直线的斜率为
，BP所在的直线的斜率为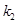
．若椭圆的离心率为
，且过点
．
（1）求
的值；
（2）求MN的最小值；
（3）随着点P的变化，以MN为直径的圆是否恒过定点，
若过定点，求出该定点，如不过定点，请说明理由．
相关试题
，对
：
和
是方程
的两个根，不等式
对任意实数
恒成立；
：函数
有两个零点，求使“
为始边作角
，它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为
的值；
求
的值.
．
时，求函数
的定义域；
的不等式
的解集是
，求
的取值范围
在其定义域内为单调递增函数，求实数
的取值范围；
，且
，若在
上至少存在一点
，使得
成立，求实数
⊥平面
；
与平面
推荐套卷
(本小题满分16分)
如图，椭圆(a>b>0)的上、下两个顶点为A、B，直线l：，点P是椭圆上异于点A、B的任意一点，连接AP并延长交直线l于点N，连接PB并延长交直线l于点M，设AP所在的直线的斜率为，BP所在的直线的斜率为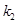．若椭圆的离心率为，且过点．
（1）求的值；
（2）求MN的最小值；
（3）随着点P的变化，以MN为直径的圆是否恒过定点，
若过定点，求出该定点，如不过定点，请说明理由．
粤公网安备 44130202000953号