吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图: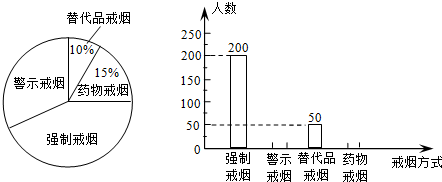
根据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
相关知识点
推荐套卷
 -
- )÷
)÷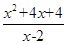 ,其中x是方程x2-2x=0的根.
,其中x是方程x2-2x=0的根.
 的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,
的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,  的平分线分别交AF、AD于点G、H.
的平分线分别交AF、AD于点G、H.
 ,
, ,求
,求 的长度;
的长度; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号