如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．
（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；
（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC的中点；
（3）如图2，在（2）的条件下，求折痕FG的长．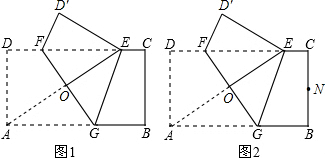
，其中
.
，其中
.
，并求
的值．
）÷（a2＋1），其中a=
－1.
）÷a，其中a=
.推荐套卷
如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．
（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；
（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC的中点；
（3）如图2，在（2）的条件下，求折痕FG的长．
粤公网安备 44130202000953号